iconCFD Optimize 2.1.1 is an extension module to iconCFD. It provides a streamlined process for the solution of optimal design problems applying ICON’s latest developments in the field of continuous adjoint optimization.
This News Cast gives a short introduction to the theory of CFD-based adjoint optimisation and presents the capabilities for adjoint topology optimization available in iconCFD Optimize 2.1.1. A second News Cast will describe adjoint shape optimization functionalities.
Adjoint Optimization
The goal of optimization in CFD is to minimize a cost function (also objective function), J (α,v,p), subject to a converged solution of the Navier Stokes Equations, R (α,v,p), in the flow domain, Ω,
![]()
by finding optimal values for a set of design parameters, α.
The adjoint method consists in using Lagrange multipliers to enforce the constraint of the Navier Stokes Equations on the optimization problem (see http://en.wikipedia.org/wiki/Lagrange_multiplier).
![]()
L (α,v,p) is the augmented cost function; the adjoint velocity, u, and the adjoint pressure, q, are the Lagrange multipliers of the problem.
Every optimal point must fulfil 3 conditions:
– A converged flow field must be obtained by solving the Navier Stokes equations:
![]()
– While α is treated as constant, an optimal point must be at a critical point of the augmented cost function:
![]()
The adjoint equations are derived from this condition (described in detail by Petropoulou [1]). They are a set of partial differential equations, from which the adjoint velocity and pressure are obtained.
– When the first two conditions are fulfilled, ![]() may be computed. This term expresses the sensitivity of the cost function with respect to the design variables. For optimal design parameters this sensitivity also becomes zero:
may be computed. This term expresses the sensitivity of the cost function with respect to the design variables. For optimal design parameters this sensitivity also becomes zero:
![]()
The major advantage of the adjoint technology over other gradient-finding methods is that the effort for computing the sensitivities (gradients) is relatively small and independent of the number of design variables.
Adjoint topology optimization in iconCFD Optimize 2.1.1
Topology optimization is used to compute an optimal geometry for internal flow problems, such as ducts. The user simply specifies the available design space. During the optimization the sensitivity information is used to iteratively block cells around the optimal flow path.

Figure 1: Topology optimisation of internal ducting system, minimizing power dissipation.
adjointSimpleFoam is a Reynolds averaged, turbulent, incompressible, steady state adjoint solver. It can be used with a variety of cost functions:
– Power dissipation (pressure loss)
– Drag
– Lift
– Flow uniformity at a surface or in a volume
– Mass flow rate
– Shear velocity (for acoustics)
– Turbulent content in a volume (for acoustics)
– Swirl in a volume
Simulations with adjointSimpleFoam can easily be set-up with the iconCFD 2.1.1 pre-processing tools.
For problems where the internal flow domain is embedded in a larger, complex geometry (i.e. a cooling duct in a car underhood), solving the optimization problem in isolation, may result in an overall non-optimal solution. In order to efficiently and accurately solve this type of problem ICON has developed the adjointSubCase technology.
With the adjointSubCase function object it is possible to solve the adjoint optimization problem locally, while solving the flow equations globally (using for example simplePorousFoam) and therefore retaining the feedback from the external flow in the optimization loop.
This method ensures appropriate flow conditions at the inlets and outlets of the sub-domain, without having to solve the adjoint equations in the whole simulation domain. Since the adjoint sub-case is created automatically at the initialisation of the simulation run, adjointSubCase is as easy to set up as any other function object.
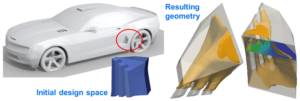
Figure 2: Click here to watch video about adjointSubCase topology optimisation of brake cooling ducts.
For further details please follow this link to contact us.
[1] S. Petropoulou, “Industrial Optimisation Solutions Based On OPENFOAM® Technology” European Conference on Computational Fluid Dynamics ECCOMAS CFD, Lisbon, Portugal, June 2010.